Unsere südlichen Nachbarn sind der Winterdepression genauso ausgesetzt, wie wir hier im Norden. Zwar scheint die Sonne im Winter länger als bei uns an der Küste, aber der verdammte Hochnebel in den Tälern treibt die Leute zur Mittagspause in die Seilbahnen, mit der sie zumindest über die Wolken kommen und ein bisschen Sonne tanken können. Warum ist diesen Nebel vorherzusagen so schwer?
Aufsteigend musst Du Dich bemühen,
Doch ohne Mühe sinkest Du.
Der liebe Gott muss immer ziehen,
Dem Teufel fällt’s von selber zu.
Wilhelm Busch
Als ich anfing mit der meteorologischen Modellierung, gab es viele Diskussionen darum, ob man die geländefolgenden Koordinaten behalten sollte oder z-Koordinaten einführen sollte, also waagerechte Koordinatenlinien, die dann aber die Berge durchkreuzen müssen und daher ihre eigenen Probleme haben. Hier ist eine Skizze der geländefolgenden Koordinaten.
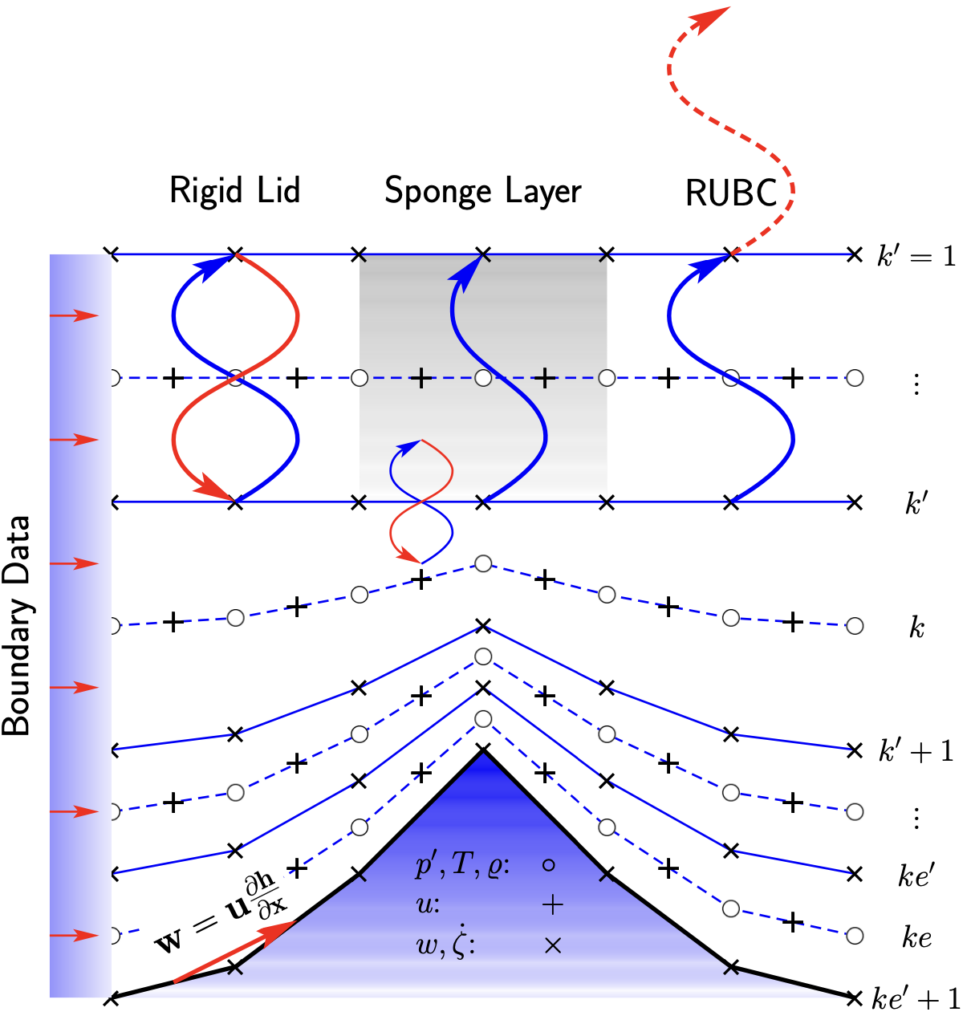
Die geländefolgenden Koordinaten können das Problem haben, dass im Fall, dass die Atmosphäre über einen Berg ruht, im Modell die wildesten Vertikalbewegungen entstehen. Das liegt daran, dass der Druckgradientterm in einem Teil entlang der Koordinatenlinien berechnet wird und dann noch eine Korrektur wegen der geländefolgenden Koordinaten ansteht.
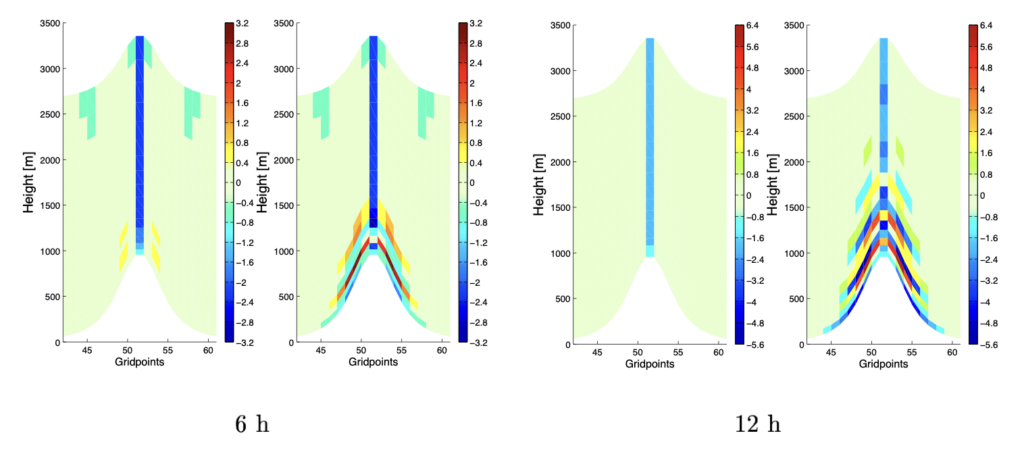
Ein massives Problem ist auch die untere Randbedingung, da man dort 
nicht mit zentrierten Differenzen berechnen kann, wie bei allen anderen Schichten. Das führt auf einen Sprung in der Fehlercharakteristik. Man kann das Problem umgehen, indem man explizit das Verschwinden der kontravarianten Vertikalgeschwindigkeit fordert. Das bedeutet, dass es keinen Fluss über den unteren Rand geben kann. Ein bisschen Algebra hat damals im COSMO Modell das Problem mit den falschen Vertikalgeschwindigkeiten sehr reduziert. Dies ist hier gezeigt für eine Gitterweite von 7 km für die korrigierte Version (links) und die Originalversion (rechts). Die Vertikalgeschwindigkeiten sind in cm/s angegeben.
Später habe ich das ICON-IAP Modell selbst entwickelt und noch höhere und steilere Berge für diesen Test benutzt. Hier ist das Resultat für einen wirklich steilen Berg.
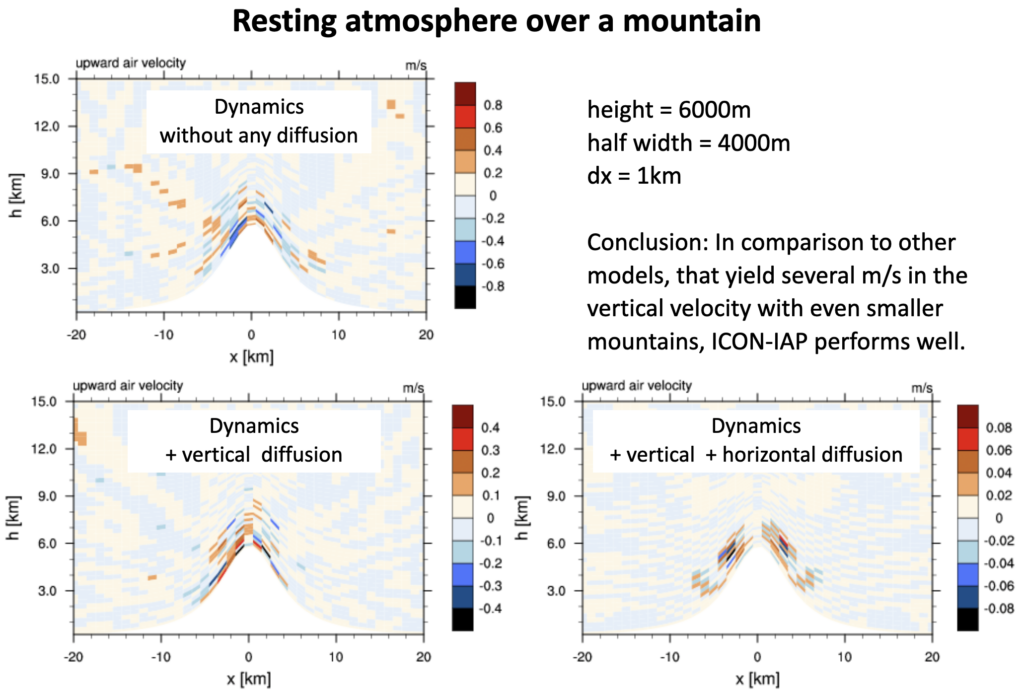
Als Fazit kann man sagen: Die genaue Spezifikation der Numerik kann die Fehler minimieren, sie gehen jedoch nie ganz weg. Bei einem Berg von 6 km Höhe und 4 km Halbwertsbreite sind Vertikalgeschwindigkeiten im einstelligen cm/s-Bereich sehr gut! Es gibt zwei Dinge, die man beachten muss
- Es gibt nur eine untere Randbedingung: die kontravariante Geschwindigkeit am unteren Rand muss verschwinden.
- Die Energieumwandlungen müssen korrekt wiedergegeben sein. Denn ist die Gesamtenergie erhalten, kann keine der beteiligten Energien (kinetische Energie, potentielle Energie, innere Energie) aus der Reihe tanzen. Für die korrekten Energieumwandlungen kann man die Hamiltonische Formulierung mit Poisson-Klammern heranziehen.
Die Atmosphäre ist ein geschichtetes Medium, daher ist der Impulsdiffusionstensor nicht mehr isotrop, sondern anisotrop. Der spurfreie Impulsdiffusionstensor ergibt sich folgendermaßen
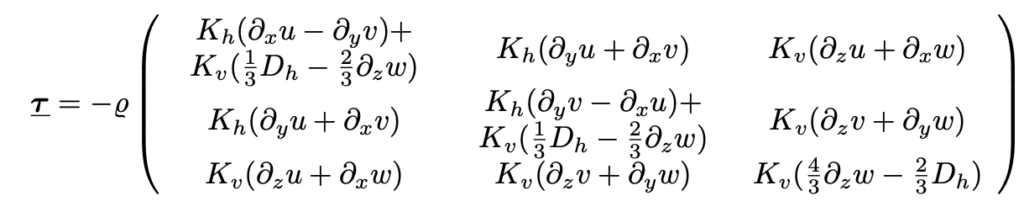
wobei horizontale und vertikale Diffusionskoeffizienten zu unterscheiden sind. Auch hier muss man die Gradienten in geländefolgenden Koordinaten formulieren und auf die unteren Randbedingungen aufpassen. Für das hexagonale ICON-IAP Modell wurde das für die horizontale Diffusion eine ziemlich komplizierte Angelegenheit. Scherungs- und Dehnungsdeformationen müssen mit speziellen Gewichten w auf den geforderten Gitterpunkten bestimmt werden.
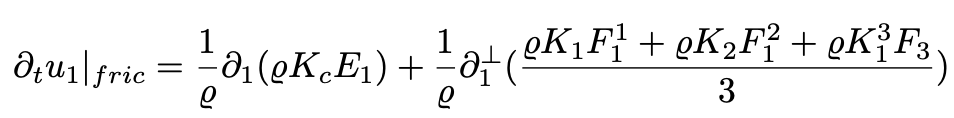
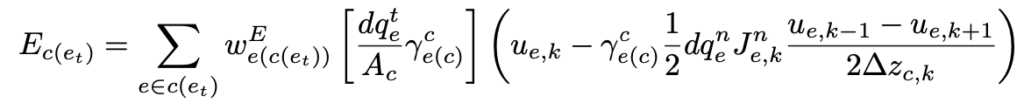
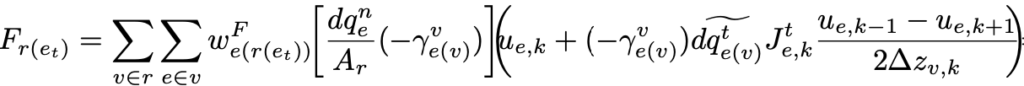
Mit diesen doch recht komplizierten Formeln ist man physikalisch konsistent unterwegs und kann auch die dann automatisch positive Scherungsproduktion als Eingang in die TKE-Gleichung richtig bestimmen.