Meteorologen sind keine Mathematiker. Sie entwickelten eine eigene Tradition numerischer Diskretisierungen. Das quadrilaterale Arakawa C-Gitter hatte sich in der meteorologischen Community zum Standard entwickelt. Geht das auch auf der Kugel? Sollten die Gitterflächen dort Dreiecke wie im deutschen ICON-Modell sein, oder etwa Hexagons und Pentagons, wie in dem US-amerikanischen MPAS-Modell?
Mit den Irrtümern der Zeit ist schwer sich abzufinden;
widerstrebt man ihnen, so steht man allein;
lässt man sich davon befangen,
so hat man auch weder Ehre noch Freude davon.
Johann Wolfgang von Goethe
Koordinatensystem mit drei Basisvektoren
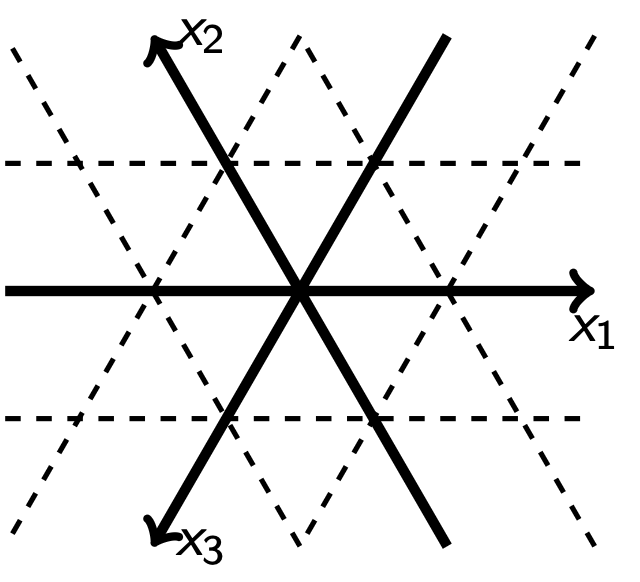
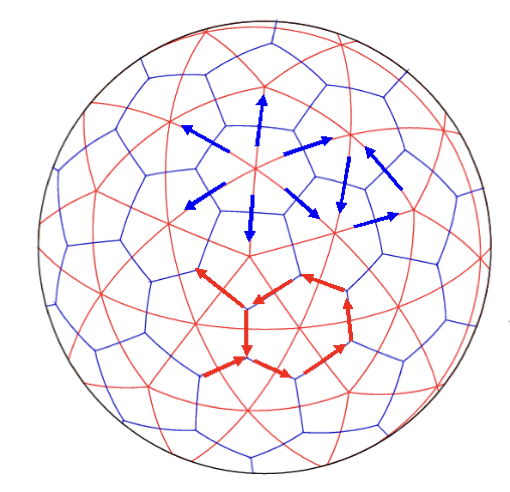
Das numerische C-Gitter positioniert skalare Werte wie Druck und Temperatur im Zentrum einer Gitterbox. Die horizontalen Geschwindigkeitskomponenten stehen senkrecht auf den Seitenflächen (oben im Bild den Kanten). Das zugehörige Koordinatensystem hat für Anwendungen auf einem ikosaederbasierten Gitter drei Richtungen. Vektoren können daher immer auf verschiedene Weisen dargestellt werden (siehe Bild weiter unten), mit roten und blauen, oder roten und schwarzen, oder schwarzen und blauen Komponenten allein. Es sind zu viele Geschwindigkeitsinformationen vorhanden. Daher muss man als mathematische Nebenbedingung fordern, dass die lineare Abhängigkeit zwischen den Geschwindigkeitskomponenten immer bestehen bleibt.
Die lineare Abhängigkeit von Vektorkomponenten kann man untersuchen, indem man das horizontale Windfeld mit der Helmholtz-Zerlegung darstellt. Diese beruht darauf, dass das horizontale Windfeld zwei verschiedene Eigenschaften hat: die horizontale Divergenz und die vertikale Komponente des Wirbels (=Vorticity). Die horizontale Divergenz ![]() kann mit dem Vektorpotential
kann mit dem Vektorpotential ![]() dargestellt werden (
dargestellt werden (![]() ) und der vertikale Wirbelanteil
) und der vertikale Wirbelanteil ![]() ist über die Stromfunktion
ist über die Stromfunktion ![]() repräsentiert (
repräsentiert (![]() ) . Dann gilt für den Windvektor
) . Dann gilt für den Windvektor ![]() , wobei
, wobei ![]() der vertikale Einheitsvektor ist. In dem trivariaten Koordinatensystem liest sich das so:
der vertikale Einheitsvektor ist. In dem trivariaten Koordinatensystem liest sich das so:
![Rendered by QuickLaTeX.com \[\latex \begin{aligned}u_1=-\sqrt{3}^{-1}(\partial_2\psi-\partial_3\psi)+\partial_1\chi\\u_2=-\sqrt{3}^{-1}(\partial_3\psi-\partial_1\psi)+\partial_2\chi\\u_3=-\sqrt{3}^{-1}(\partial_1\psi-\partial_2\psi)+\partial_3\chi\end{aligned}\]](https://almut-gassmann.de/wp-content/ql-cache/quicklatex.com-cf6bdde863450b2753bef4eaa00fbc35_l3.png)
Wegen der linearen Abhängigkeit ist ![]() , insbesondere gilt
, insbesondere gilt ![]() . Wie überträgt man diese kontinuierliche Darstellung auf die diskrete Darstellung?
. Wie überträgt man diese kontinuierliche Darstellung auf die diskrete Darstellung?
Die diskrete Darstellung wird im Folgenden mit einem Hütchensymbol ![]() angezeigt. Die Orte der Geschwindigkeitskomponenten
angezeigt. Die Orte der Geschwindigkeitskomponenten ![]() befinden sich an den Kanten einer Gitterbox. Die Orte von
befinden sich an den Kanten einer Gitterbox. Die Orte von ![]() und
und ![]() können nur die Zentren der Hexagons sein, denn nur dann stimmt die Anzahl der sinnvollen Freiheitsgrade: Es gibt drei
können nur die Zentren der Hexagons sein, denn nur dann stimmt die Anzahl der sinnvollen Freiheitsgrade: Es gibt drei ![]() statt der üblichen zwei
statt der üblichen zwei ![]() Freiheitsgrade in der Repräsentation der Geschwindigkeitskomponenten, also muss es auch genau zwei Freiheitsgrade in
Freiheitsgrade in der Repräsentation der Geschwindigkeitskomponenten, also muss es auch genau zwei Freiheitsgrade in ![]() geben. Das geht nur, wenn diese auf den Zentren der Hexagons positioniert werden.
geben. Das geht nur, wenn diese auf den Zentren der Hexagons positioniert werden.
Nun steht die Aufgabe, die Geschwindigkeitskomponenten ![]() von den Kanten „irgendwie“ zum Zentrum eines Hexagons zu mitteln. John Thuburn von der Universität Exeter fand 2008 eine solche Mittelung, die nun mit
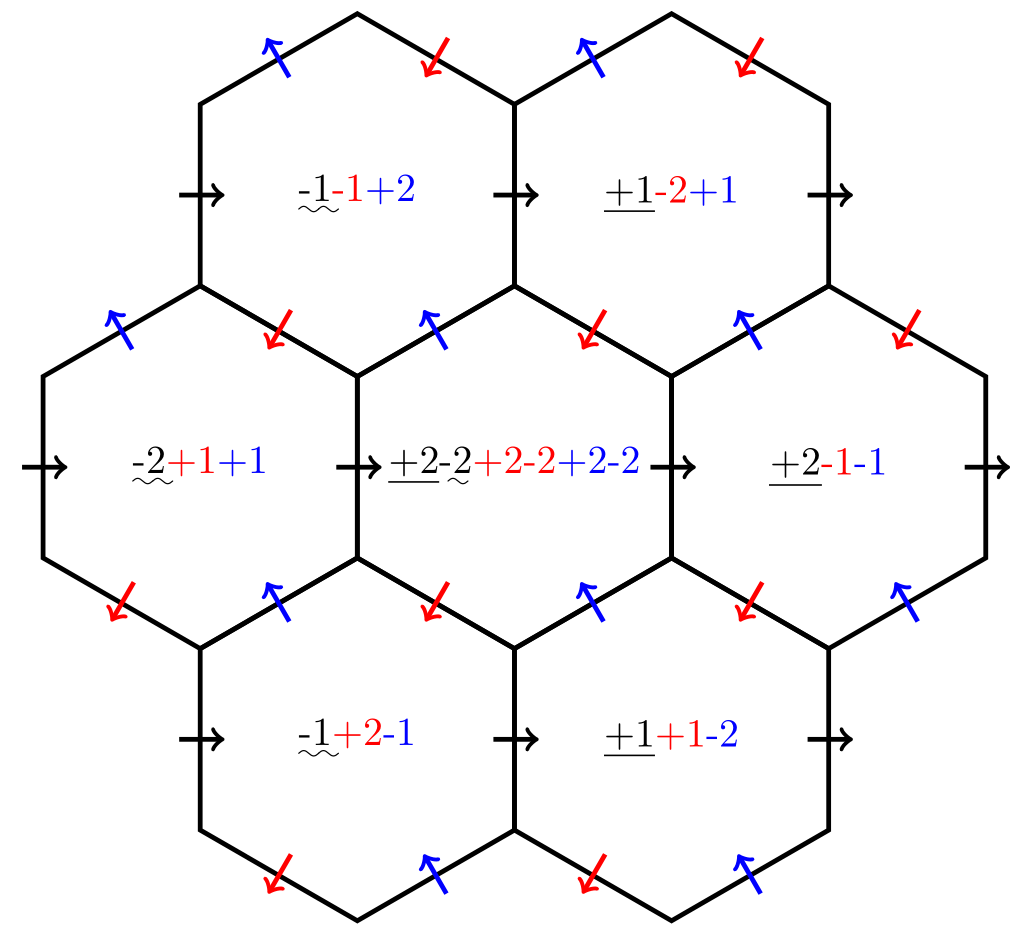
von den Kanten „irgendwie“ zum Zentrum eines Hexagons zu mitteln. John Thuburn von der Universität Exeter fand 2008 eine solche Mittelung, die nun mit ![]() symbolisiert wird. Im Bild deuten die unterstrichenen Zahlen die Anteile (in Sechstel) an, mit denen man
symbolisiert wird. Im Bild deuten die unterstrichenen Zahlen die Anteile (in Sechstel) an, mit denen man ![]() zunächst auf die Kante von Koordinatenachse 1 mitteln muss, bevor man den nun diskreten Gradienten ausrechnet. Die Summe
zunächst auf die Kante von Koordinatenachse 1 mitteln muss, bevor man den nun diskreten Gradienten ausrechnet. Die Summe ![]() ist tatsächlich null. Man kann die einzelnen Summanden von
ist tatsächlich null. Man kann die einzelnen Summanden von ![]() in jeder Gitterbox darstellen, und wie im Bild gezeigt, ergeben sie in jeder Gitterbox in der Summe null. Die lineare Abhängigkeitsregel überträgt sich automatisch auf den Wirbelanteil des Windfeldes, wenn schon in diesen Termen die Thuburn-Mittelung angewendet wird
in jeder Gitterbox darstellen, und wie im Bild gezeigt, ergeben sie in jeder Gitterbox in der Summe null. Die lineare Abhängigkeitsregel überträgt sich automatisch auf den Wirbelanteil des Windfeldes, wenn schon in diesen Termen die Thuburn-Mittelung angewendet wird
![Rendered by QuickLaTeX.com \[\latex\begin{aligned}\widetilde{\hat{u}_1}^1=-{\sqrt{3}}^{-1}(\hat\partial_2\widetilde{\hat\psi}^{31}-\hat\partial_3\widetilde{\hat\psi}^{21})+\hat\partial_1\widetilde{\hat\chi}^1\\\widetilde{\hat{u}_2}^2=-{\sqrt{3}}^{-1}(\hat\partial_3\widetilde{\hat\psi}^{12}-\hat\partial_1\widetilde{\hat\psi}^{32})+\hat\partial_2\widetilde{\hat\chi}^2\\\widetilde{\hat{u}_3}^3=-{\sqrt{3}}^{-1}(\hat\partial_1\widetilde{\hat\psi}^{23}-\hat\partial_2\widetilde{\hat\psi}^{13})+\hat\partial_3\widetilde{\hat\chi}^3\end{aligned}\]](https://almut-gassmann.de/wp-content/ql-cache/quicklatex.com-4b90f7afd35718ca13eb9b69bf97c102_l3.png)
Ein interessanter Aspekt der linearen Abhängigkeitsregel ist, dass man die Summe ![]() uminterpretieren kann in die Aussage, dass es kein Schachbrettmuster im Wirbel des Windes gibt, wenn man die Wirbel als Umlaufintegral um die Kanten von Dreiecken ausrechnet: Für die Dreiecke mit der Spitze nach oben gilt
uminterpretieren kann in die Aussage, dass es kein Schachbrettmuster im Wirbel des Windes gibt, wenn man die Wirbel als Umlaufintegral um die Kanten von Dreiecken ausrechnet: Für die Dreiecke mit der Spitze nach oben gilt ![]() und für die Dreiecke mit der Spitze nach unten gilt
und für die Dreiecke mit der Spitze nach unten gilt ![]() . Ein Hexagonzentrum
. Ein Hexagonzentrum ![]() wird von je drei nach oben und nach unten zeigenden Dreiecken umgeben, und man findet
wird von je drei nach oben und nach unten zeigenden Dreiecken umgeben, und man findet ![]() . Das heißt, dass die Summe der drei nach oben zeigenden Dreiecksvorticities gleich die Summe der drei nach unten zeigenden Dreiecksvorticities ist. Anschaulich bedeutet dass, dass es kein Schachbrettmuster gibt. Diese Eigenschaft kann man ausnutzen, wenn das Gitter leicht verformt ist, denn auf der Kugel ist das reguläre Gitter nicht anzutreffen. Diese Schachbrettvermeidungsregel ist in der inzwischen Standard gewordenen TRiSK-Vektorrekonstruktion für die Tangentialgeschwindigkeit im Coriolisterm numerisch umgesetzt.
. Das heißt, dass die Summe der drei nach oben zeigenden Dreiecksvorticities gleich die Summe der drei nach unten zeigenden Dreiecksvorticities ist. Anschaulich bedeutet dass, dass es kein Schachbrettmuster gibt. Diese Eigenschaft kann man ausnutzen, wenn das Gitter leicht verformt ist, denn auf der Kugel ist das reguläre Gitter nicht anzutreffen. Diese Schachbrettvermeidungsregel ist in der inzwischen Standard gewordenen TRiSK-Vektorrekonstruktion für die Tangentialgeschwindigkeit im Coriolisterm numerisch umgesetzt.
Die Schachbrettfreiheit der Vorticity auf Dreiecken ist also ein mathematischer Aspekt, der aus der linearen Abhängigkeit der Geschwindigkeitskomponenten im regulären Gitter als Eigenschaft auf ein deformiertes Gitter als Constraint übertragen wird.
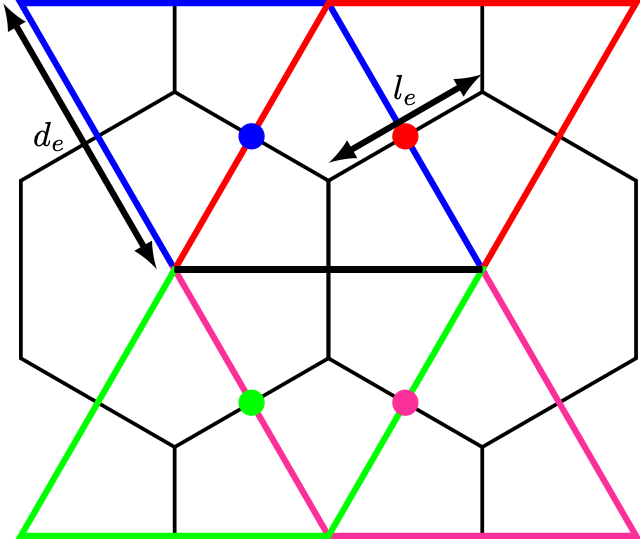
Aus physikalischer Sicht, unter anderem der Dispersionsrelation der Flachwasserwellen, stellt sich jedoch heraus, dass die Vorticity auf Rhomben, also zwei verbundenen Dreiecken, relevant ist. Auf dem Bild ist mit den bunten Kanten der Umlaufweg um das jeweilige mit dem dicken Punkt angedeutete Zentrum des Rhombus angedeutet. Die schwarze Kante trägt alle Farben. Man findet für die Vorticity auf Rhomben ein diskretes Äquivalent zu ![]() , nämlich zum Beispiel für den Rhombus an Kante 1 (in der Mitte des Bildes):
, nämlich zum Beispiel für den Rhombus an Kante 1 (in der Mitte des Bildes):
![Rendered by QuickLaTeX.com \[\latex\begin{aligned}\hat\zeta_1&=\frac{2}{\sqrt{3}}(\hat\partial_2\hat{u}_3-\hat\partial_3\hat{u}_2)\\&=\frac{2}{\sqrt{3}}(\hat\partial_2(-\frac{1}{\sqrt{3}}(\hat\partial_1\widetilde{\hat\psi}^2-\hat\partial_2\widetilde{\hat\psi}^1)+\hat\partial_3\hat\chi)-\hat\partial_3(-\frac{1}{\sqrt{3}}(\hat\partial_3\widetilde{\hat\psi}^1-\hat\partial_1\widetilde{\hat\psi}^3)+\hat\partial_2\hat\chi))\\&=\frac{2}{3}(\hat\partial_{22}\widetilde{\hat\psi}^1+\hat\partial_{33}\widetilde{\hat\psi}^1-\hat\partial_{12}\widetilde{\hat\psi}^2-\hat\partial_{13}\widetilde{\hat\psi}^3)\\&=\frac{2}{3}(\hat\partial_{22}\widetilde{\hat\psi}^1+\hat\partial_{33}\widetilde{\hat\psi}^1-\hat\partial_{1}(\hat\partial_2\widetilde{\hat\psi}^2+\hat\partial_{3}\widetilde{\hat\psi}^3))\\&=\frac{2}{3}(\hat\partial_{11}\widetilde{\hat\psi}^1+\hat\partial_{22}\widetilde{\hat\psi}^1+\hat\partial_{33}\widetilde{\hat\psi}^1)=\hat\nabla^2\widetilde{\hat\psi}^1\end{aligned}\]](https://almut-gassmann.de/wp-content/ql-cache/quicklatex.com-6c7ca7d50d39b210322471610c9a9c93_l3.png)
Und obendrein findet man damit ganz einfach, dass ![]() . Diesen Zusammenhang braucht man beim Beweis, dass auch für den um einen konstanten Grundstrom linearisierten verallgemeinerten Coriolisterm die lineare Abhängigkeit gewährleistet bleiben kann. Dann darf in diesem Term für die Windkomponente an Kante 1 nur die im Bild bunt dargestellten Rhombusvorticities benutzen. In der Folge wird die aus den kontinuierlichen Gleichungen bekannte Äquivalenz
. Diesen Zusammenhang braucht man beim Beweis, dass auch für den um einen konstanten Grundstrom linearisierten verallgemeinerten Coriolisterm die lineare Abhängigkeit gewährleistet bleiben kann. Dann darf in diesem Term für die Windkomponente an Kante 1 nur die im Bild bunt dargestellten Rhombusvorticities benutzen. In der Folge wird die aus den kontinuierlichen Gleichungen bekannte Äquivalenz ![]() , also die Äquivalenz von vektorinvarianter Form und Advektionsform, weitestgehend erfüllt. Die Advektionsform ist die Voraussetzung dafür, dass man versteht, wie Verfahren höherer Ordnung, die die numerischen Dispersionsfehler der Advektion bekämpfen, formuliert werden können.
, also die Äquivalenz von vektorinvarianter Form und Advektionsform, weitestgehend erfüllt. Die Advektionsform ist die Voraussetzung dafür, dass man versteht, wie Verfahren höherer Ordnung, die die numerischen Dispersionsfehler der Advektion bekämpfen, formuliert werden können.
Diese bedeutungsmäßige Unterscheidung der Vorticity auf Dreiecken (mathematischer Aspekt wegen der überspezifizierten Geschwindigkeitskomponenten und daher Grundlage der TRiSK Vektorrekonstruktion) und der Vorticity auf Rhomben (physikalischer Aspekt in der Dispersionsrelation und in der Advektion des Impulses) ist den meisten Autoren nicht bewusst.
Weil für die linearisierten Gleichungen kein Schachbrettmuster des Wirbels auf Dreiecken auftreten kann, bedeutet dies im Umkehrschluss, dass das tatsächliche Auftreten eines Schachbrettmusters ein Zeichen einer nichtlinearen Energiekaskade ist, wobei durch nichtlineare Advektion des Windes mit dem Wind immer kleinere Skalen entstehen. Diese kleineren Skalen gehören nicht mehr zur nominellen Auflösungsskala des Modells.
Zusammenfassung der Konsequenzen der linearen Abhängigkeit
- Die Divergenz ist auf Hexagons definiert.
- Der Wirbel (im physikalischen Sinn) ist auf Rhomben definiert.
- Im linearen Fall gibt es kein Schachbrettmuster des Wirbels auf Dreiecken.
- Schachbrettmuster im Wirbel auf Dreiecken im nichtlinearen Fall sind Zeugnis der Energiekaskade hin zu kleineren Skalen.
- Die Forderung der Schachbrettfreiheit der Wirbel auf Dreiecken ist der Hintergrund der TRiSK-Vektorrekonstruktion im deformierten Gitter, welches man auf der Kugel antrifft.
- Die Vorticity auf Dreiecken gehört nicht zum Modelloutput. Nur die Vorticity auf Rhomben, also an Kantenpunkten, ist ein physikalisch sinnvoller Modelloutput.
So sehen Ergebnisse mit dem hexagonalen Model aus
Hier ist ein Vergleich verschiedener Modellkonzeptionen, die sich in der nichtlinearen Advektion des Impulses unterscheiden. Gezeigt ist die absolute Vorticity im Flachwassermodell auf dem äquilateralen Gitter. Die G18 Methode ist die oben erwähnte Methode, bei der die vektorinvariante Form der Impulsadvektion der advektiven Form fast perfekt entspricht. Nur die Abbildung rechts unten benutzt eine Methode, die, wie die Mathematiker sagen, von höherer Ordnung ist.
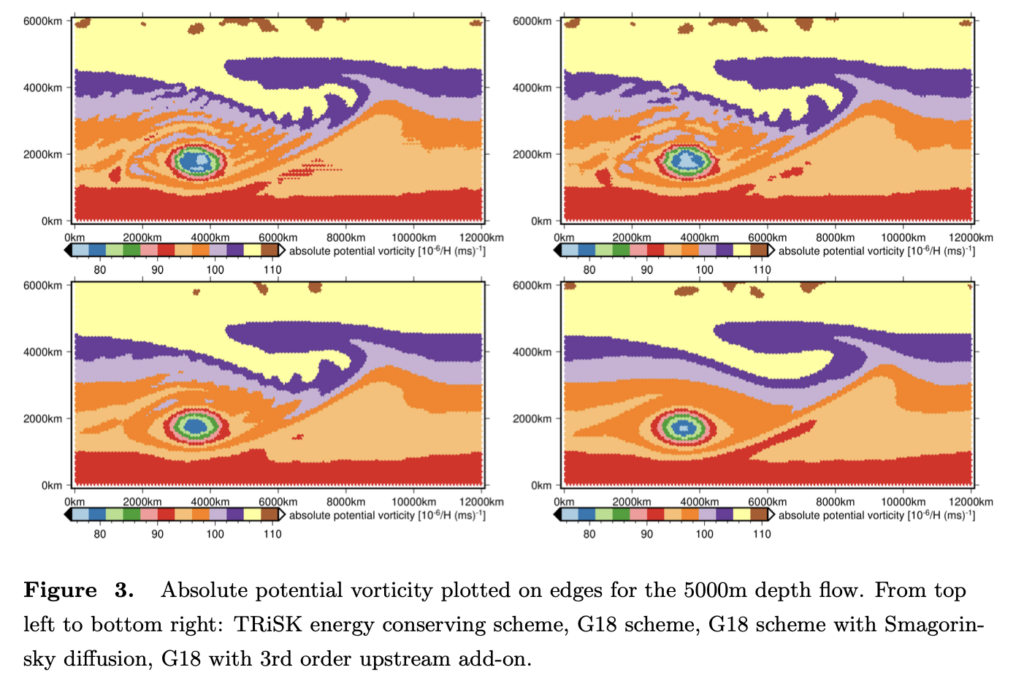
Die Methode höherer Ordnung vermindert auch die Entstehung von Schwerewellen aufgrund von den in der Numerik bekannten Dispersionsfehlern. Dies funktioniert auch auf dem deformierten Gitter auf der Kugel: Farbig dargestellt sind die Ergebnisse mit dem Verfahren höherer (3.) Ordnung, die überlagerten Konturen sind Ergebnisse mit dem Verfahren 2. Ordnung ohne (links) und mit (rechts) zusätzlicher Diffsion. Die Methode höherer Ordnung hat die geringsten Signaturen von fälschlich erzeugten Schwerewellen.
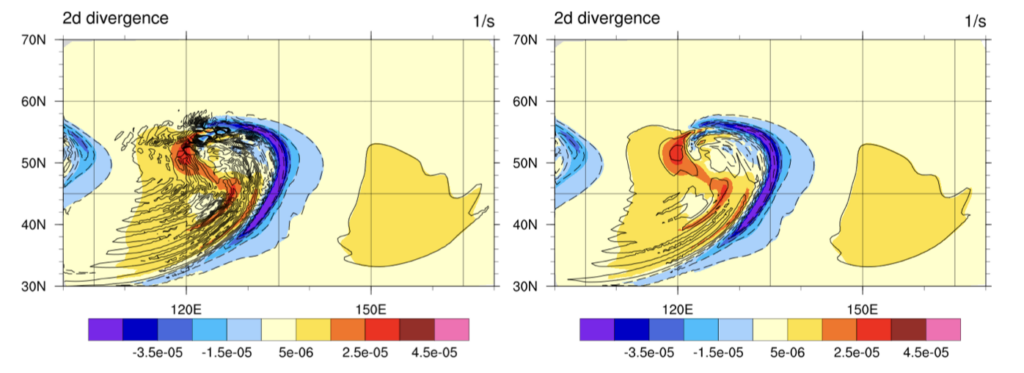
Was ist daher an ICON falsch?

ICON definiert die Hauptgitterpunkte auf Dreiecken. Im Vergleich zum hexagonalen C-Gitter befinden sich die Geschwindigkeitskomponenten an den gleichen Orten, sind aber um 90° gedreht.
Die Abbildung zeigt das Muster des Divergenzfeldes bei der Testaufgabe, einen zonalen Grundstrom zu simulieren, ein lineares Problem!
ICON hat folgende konzeptionellen Probleme:
- Die prognostischen Geschwindigkeitskomponenten können nicht linear abhängig gehalten werden, da die Gradientkomponenten dies nicht hergeben.
- Es ergibt sich schon im linearen Fall (und nicht erst im nichtlinearen Fall wie oben bei den Hexagons beschrieben) ein Schachbrettmuster der Divergenz auf Dreiecken.
- Die Rekonstruktion der Tangentialgeschwindigkeit für den Coriolisterm könnte ebenso wie im hexagonalen C-Gitter erfolgen. Die Vektorkomponenten sind ja nur um 90° gedreht. Implementiert ist aber eine RBF-Rekonstruktionsvariante, die mit Scheuklappenblick die Einbettung in die Gesamtnumerik ignoriert.
- Es gibt doppelt so viele Dreiecke wie Sechsecke, daher müssen die Parametrisierungen subskaliger Prozesse bei gleicher numerischer Auflösung des Geschwindigkeitsfeldes doppelt so häufig berechnet werden wie im hexagonalen C-Gitter. Das erhöht den Rechenaufwand immens.
- Korrekte Energieumwandlungen zwischen kinetischer Energie (Druckgradientterm) und innerer Energie (Kompressionsterm) darzustellen, wird erheblich erschwert.
- Das Bügeleisen, welches das Schachbrettmuster plättet, widerspricht der Intention derer, die das C-Gitter einst erfanden. Sie taten das, um inhärente Mittelungen zu vermeiden, die auf anderen Gitterstaffelungsarten unvermeidlich sind und zu größeren numerischen Fehlern in der Wellenausbreitung führen.
- Den Glättungsoperator, der benötigt wird, um das Schachbrettmuster zu verstecken, kann man nicht alternativ als Impulsdiffusionsoperator darstellen. Daher gibt es Schwierigkeiten mit der Entropiebilanz und mit der Wellendispersionrelation im dreidimensionalen Fall, da man ja eine horizontale Divergenz aus numerischen Gründen dämpft, der Impulsdiffusionsoperator aber nur eine dreidimensionale Divergenzdämpfung beinhaltet. Dieses Problem war schon im COSMO-Modell aufgetreten.
- Die benutzte vektorinvariante Form der Impulsadvektion lässt sich nicht näherungsweise in eine advektive Form umformulieren. Damit verliert man die Möglichkeit, durch Zusatzterme eine Methode von höherer Ordnung abzuleiten, die die Dispersionsfehler bekämpft.
Im Vergleich der beiden Gitter schneidet also das hexagonale C-Gitter bedeutend besser ab: Es ist in seinen Eigenschaften äquivalent zu dem früher üblichen quadrilateralen C-Gitter. Auftretende Schachbrettmuster in Divergenz beziehungsweise Wirbel haben sehr verschiedene Ursachen: Das Schachbrett in der Divergenz auf dem triangulären C-Gitter ist ein Ausdruck einer falschen Numerik. Das Schachbrett im Wirbel im hexagonalen C-Gitter ist ein Ausdruck einer nichtlinearen Energiekaskade.
Warum diese altmodischen finiten Volumen?
Numerische Methoden schauen sehr häufig nur auf die Differentialgleichungen an sich. Ein großes Ziel ist dann, die numerischen Fehler zu vermeiden. Daher sind Verfahren, die von höherer Ordnung sind (spektrale Elemente, discontinuous Galerkin) sehr beliebt. Allerdings können die Randbedingungen für jedes einzelne Luftvolumen nur durch Flüsse über den Rand hergestellt werden. Von der Unterlage (Boden, Ozean) können wir nur flächengemittelte Flüsse darstellen. Vom Blick der Thermodynamik her müssen wir jedes Teilgebiet als abgeschlossenes Volumen behandeln können. Kurzum, die Frage, wie wir auch die irreversiblen Prozesse in sich konsistent in ein numerisches Verfahren integrieren können, erscheint mir persönlich auf die finiten Volumen Methode als Methode der Wahl zu deuten. Ich lasse mich aber gern eines Besseren belehren.
Warum rechnet ICON nicht auf Hexagons, sondern auf Dreiecken, auch wenn man vieles früh genug wusste?
Hier sind meine Überlegungen dazu. Sie sprechen sowohl sachliche Punkte als auch psychologische Aspekte an. Wir blenden so häufig aus, dass wir als Menschen vor allem in einer sozialen Umgebung leben, und diese bestimmt, was geschieht, nicht die Logik der Mathematik oder Physik.
- Man hatte anfangs schon mal die Hexagons ausprobiert (Doktorarbeit von William Sawyer), aber kannte die Thuburn-Mittelung nicht. Daher konnte man keine sinnvollen Wirbelfelder simulieren, und schloss daraus, dass es nur mit den Dreiecken geht.
- Man hat sich der wissenschaftlichen Diskussion verweigert, es nicht erlaubt, die Entwickler der TRiSK-Vektorrekonstruktion in die Suche nach optimalen Verfahren einzubinden: „Wir wollen uns von den anderen absetzen.“
- Man wollte eben die schnelle Entwicklung, um etwas Vorzeigbares zu haben. Ich frage mich aber, vor welchem Direktor meine Vorgesetzten diese Schnelligkeit rechtfertigen mussten. Gab es da überhaupt jemanden, gegenüber dem sie wirklich rechenschaftspflichtig waren?
- Leider hatte ich am Anfang selbst noch nicht verstanden, wie man die nichtlineare Advektion des Impulses diskretisiert. Meine Ergebnisse mit den Hexagons nicht so super, wie sie jetzt sind. Daher sagte man: „Jedes Modell hat eben seine Fehler, da ist es doch einerlei, welches wir nehmen.“
- Eine Fehlüberlegung war, dass man die Reihenfolge, mit der man Optionen ausschließt oder durchlässt, missachtet hat. Die richtige Reihenfolge hätte sein müssen:
- Ist das lineare Problem in Ordnung?
- Ist das nichtlineare Problem in Ordnung?
- Wie geht die Gitterverfeinerung?
- Man wollte die hierarchische Gitterverfeinerung. Dies schien mit den Dreiecken besser zu gehen. Hans Herzog, mein Freund und Co-Autor, sagt dazu: „Man hat das Pferd von hinten aufgezäumt.“ Hierarchische Gitterverfeinerung ginge auch mit dem hexagonalen Gitter, aber man muss dafür verstehen, wie genau die physikalischen Vorticities auf dem Gitter definiert sind. Die Entwickler des MPAS-Modells haben sich für eine Gitterstreching-Variante statt für eine hierarchische Verfeinerungsvariante entschieden. Das wäre auch bei ICON gegangen, und war in einem Flachwasser-Prototypmodell schon ausprobiert worden (Doktorarbeit von Werner Bauer).
- Der Gutachter Dave Randall von der Colorado State University sagte während der Evaluierung des Max-Planck-Institutes für Meteorologie im November 2008 zu Bjorn Stevens, einem der Direktoren: „Am Ende wird euch nichts anderes übrig bleiben, als die Hexagons zu nehmen.“ Und Dave Randall ist wirklich ein Kenner der Materie!
- Die internationale Modellierungscommunity hat früh und häufig genug gewarnt. In den online nachzulesenden Gutachten des Papers The ICON-1.2 hydrostatic atmospheric dynamical core on triangular grids – Part 1: Formulation and performance of the baseline version wird die Wahl des Gitters nicht nur von mir ausgiebig beklagt. Leider konnte die Hauptautorin dieses Papers, Hui Wan, nicht am DCMIP-Workshop 2008 in Boulder und nicht an der „PDEs on the sphere“ Konferenz 2009 in Santa Fe teilnehmen, da die US-amerikanische Administration ihr als Chinesin die Einreise verweigerte. Dadurch bekam sie nicht aus erster Hand mit, was dort genau diskutiert wurde. Auf dem DCMIP-Workshop 2008 waren praktisch alle Anwesenden von John Thuburns neuer Mittelungsmethode quasi wie elektrisiert und haben gejubelt — schon bei der Icebreaker reception.
- Pedro da Silva Peixoto, Mathematikprofessor von der Universität Sao Paulo, saß im Pub beim Bier und sagte zu einem anderen Konferenzteilnehmer: „Du kannst in der Numerik alles machen, was du willst, aber mach es bloß nicht wie die Deutschen. Never do this!“ Auch von anderen Seiten kommt Kritik: Im Review über das ICON-Sapphire Projekt wundern sich die Gutachter über große Energie-Imbalancen. Im Review vom Paper über die Gitterverfeinerung von ICON verbittet sich ein Gutachter zu behaupten, die Gitterverfeinerung wäre zu kompliziert mit einem hexagonalen Grundgitter.
- Ich habe in mehrmaligen Versuchen, diese Entwicklung noch abzuwenden, gegen Wände geredet und konnte nichts erreichen, außer dass ich mich selbst in enormen psychischen Stress versetzt habe, dessen Folgen mich nur noch mehr in die Ecke gedrängt haben: „Seht, was für ein Mensch sie ist, sie hat noch nicht mal ihre Gefühle unter Kontrolle.“ Bei einem dieser Argumentationsversuche kam auf meine Erwähnung, dass die Parametrisierungen doppelt so häufig und daher teuer errechnet werden müssen, vom Vorgesetzten das Argument: „Das ist doch gut, dann haben wir mehr Subgridskalenvariabilität.“
- Ich rechne es Bjorn Stevens hoch an, dass er sich 2023 für eine Aussöhnung mit mir Zeit genommen hat. Danke!
- Ich verstehe meine ehemaligen Kollegen nicht. Sie nicht zu verstehen, ist eines der größten ungelösten Rätsel für mich. Wenn ich sie frage, sind die Antworten: „Wieso, ist doch nicht so schlimm, es funktioniert doch.“ oder: „Du bist einfach zu wenig kompromissbereit und zu wenig pragmatisch.“ oder: „Wir sind halt Ingenieure und keine Wissenschaftler.“ oder: „Du bist eine Fundamentalistin und akzeptierst die Sichtweisen anderer nicht.“ oder: „Die Verifikationsergebnisse sind doch top!“ (Nach Sir Karl Popper geht es aber immer um Falsifikation, und nicht um Verifikation. Verifikation in der Meteorologie heißt, den Modelloutput mit den Messdaten zu vergleichen. Das ist ein integraler Vergleich, in dem die Wirkungen der Numerik, der physikalischen Parametrisierungen und der Datenassimilation nicht mehr zu trennen sind. Offensichtlich ist erstaunlich und erfreulich gut in den Bereichen Datenassimilation und Parametrisierungen gearbeitet worden. Hut ab vor denjenigen Mitarbeitern, die dies erreicht haben.)
- Ein Grund meiner Kündigung der Arbeit am Institut für Atmosphärenphysik (IAP) in Kühlungsborn, wo ich schließlich eine ICON-Variante auf Hexagons implementiert hatte, war, dass mit dem Direktorenwechsel 2021 eine Annäherung an die Community-Modellierung mit ICON absehbar war. Ich habe für mich keinen Platz mehr dort gesehen. Tatsächlich wird jetzt am IAP mit ICON modelliert — wie vielerorts in Deutschland.
- Ich glaube, wenn Günther Doms noch gelebt hätte, wäre das alles nicht so gekommen. Mit ihm hätte ich einen wirklichen Experten an meiner Seite gehabt. Ihn hätte man nicht so einfach ignorieren können. Gott hab ihn selig.
Alle Menschen reagieren zuerst mit den Gefühlen und dann mit dem Verstand. Das hat die Evolution so eingerichtet. Ein Freund hat mal gesagt: „Du kannst Dich mit Leuten in der Sache fetzen, wie du willst. Aber Du musst am Abend mit ihnen in der Kneipe zusammen ein Bier trinken können.“
Wichtige Paper zum Nachlesen
- Geostrophic Adjustment and the Finite-Difference Shallow-Water Equations: Standard-Wissen eines Atmophärenmodellierers über Arakawa-Gitterstaffellungen im Jahr 1994
- Geostrophic Adjustment on Hexagonal Grids: Wissensstand um 2002
- Analysis of Discrete Shallow-Water Models on Geodesic Delaunay Grids with C-Type Staggering: Erstes Paper über ICON, Flachwassermodell
- A Consistent Time-Split Numerical Scheme Applied to the Nonhydrostatic Compressible Equations: Hier zeigten Hans Herzog und ich, dass horizontale Divergenzdämpfung zu fehlerhafter Dispersionsrelation von Schwerewellen im dreidimensionalen Modell COSMO führt.
- Numerical wave propagation on the hexagonal C-grid: Das Thuburn-Mittelungspaper
- Numerical representation of geostrophic modes on arbitrarily structured C-grids: TRiSK I
- A unified approach to energy conservation and potential vorticity dynamics for arbitrarily-structured C-grids: TRiSK II
- Inspection of hexagonal and triangular C-grid discretizations of the shallow water equations: Mein Versuch, durch die Blume zu sagen, dass Dreiecke Mist sind.
- Conservative Transport Schemes for Spherical Geodesic Grids: High-Order Flux Operators for ODE-Based Time Integration: Paper über Advektion von höherer Ordnung von skalaren Variablen: eine Zusammenarbeit mit Bill Skamarock. Diese Zusammenarbeit war ein politisches Vabanquespiel, weil Bill Skamarock zu den TRiSK-Leuten gehörte, von denen wir uns ja absetzen sollten.
- The ICON-1.2 hydrostatic atmospheric dynamical core on triangular grids – Part 1: Formulation and performance of the baseline version: Hui Wans Paper über das hydrostatische ICON mit den nachlesbaren Kritiken der Gutachter am gewählten Gitter
- A global hexagonal C-grid non-hydrostatic dynamical core (ICON-IAP) designed for energetic consistency: Meine nichthydrostatische Variante auf Hexagons, wo aber noch die Hollingsworth-Instabilität (nichtlineare Instabilität) drin war
- The ICON (ICOsahedral Non-hydrostatic) modelling framework of DWD and MPI-M: Description of the non-hydrostatic dynamical core: Das nichthydrostatische ICON des DWD auf dem triangulären C-Gitter
- Formulation of an unstructured grid model for global ocean dynamics: Das ICON-Ozean Modell will zeigen, dass ein trianguläres C-Gitter möglich ist. Es wird nicht erwähnt, dass das C-Gitter einst wegen der relativ guten Schwerewellendispersionseigenschaften, die aufgrund von Vermeidung von inhärenten Mittelungen erreicht werden, propagiert wurde.
- A Multiscale Nonhydrostatic Atmospheric Model Using Centroidal Voronoi Tesselations and C-Grid Staggering: Das US-amerikanische MPAS-Modell auf dem hexagonalen C-Gitter
- Discretization of generalized Coriolis and friction terms on the deformed hexagonal C-grid: Meine Neuformulierung der Impulsadvektion, wobei
 der Clou war und plötzlich alles wirklich perfekt aussah.
der Clou war und plötzlich alles wirklich perfekt aussah. - Third-order momentum advection on the quasi-hexagonal C-grid on the sphere: Dieses Paper habe ich nur eingereicht und konnte, weil ich nicht mehr am IAP arbeitete, die von den Gutachtern geforderten Verbesserungen aus Zeit- und Ressourcenmangel nicht mehr durchführen. Dort ist eine Variante der Advektion höherer Ordnung für den Impuls vorgestellt, die die Dispersionsfehler vermeidet. Bisher ist die Methode noch in keinem Modell auf der Welt, welches auf Hexagons arbeitet, operationell umgesetzt worden.
- Simulation of tropical-cyclone-like vortices in shallow-water ICON-hex using goal-oriented r-adaptivity: Hier (Doktorarbeit von Werner Bauer) wird in einem Flachwasser-Prototypmodell gezeigt, dass variable Auflösung durch ein Gitterstrechingverfahren möglich ist.
- Implementing the HYbrid MAss flux Convection Scheme (HYMACS) in ICON – First idealized tests and adaptions to the dynamical core for local mass sources: Im voll entwickelten ICON-Modell mit Konvektion werden die vorherzusehenden Probleme der künstlichen Dämpfung der horizontalen Divergenz offensichtlich.
- offizielle ICON Webseite