Tja, wie halten es die Meteorologen mit dem zweiten Hauptsatz der Thermodynamik? In der Natur gibt es kein perpetuum mobile. Daher wird immer irgendwo Entropie erzeugt. Wo genau ist das in numerischen Modellen der Atmosphäre repräsentiert? Und ist das überhaupt wichtig?

But if your theory is found to be against the Second Law of Thermodynamics I can give you no hope; there is nothing for it to collapse in deepest humiliation.”
Arthur Stanley Eddington

We have missing processes in our models. Where is the frictional heating of falling rain?
Dave Randall in Banff 2019

Die Meteorologen haben Probleme, die Begriffe Auftrieb, Arbeit, Wärme, Entropie im Modellierungskontext richtig zu verwenden. Das führt nicht unbedingt auf falsche Resultate von Modellrechnungen, aber auf gefährlich tradiertes Halbwissen, welches man dann eben glauben, und nicht verstehen muss.

Geneigter Leser, oder geneigte Leserin! Ich möchte hier niemanden persönlich angreifen. Unterschiedliche Communities haben auch an unterschiedlichen Stellen Probleme: die französischen Probleme sind nicht die der Deutschen und die des Nordens nicht die des Südens. Und ich hab natürlich meine eigenen Verständnisprobleme.

Turbulenz und Entropie in der atmosphärischen Modellierung

Im Studium bekommt man gesagt: Wir beobachten, dass Tracer turbulent gemischt werden. Die potentielle Temperatur ist ein Tracer, genauso wie der spezifische Wasserdampfgehalt.

Im Folgenden wollen wir aber nur den trockenen Fall betrachten, alles andere irritiert vorerst die Argumentationskette. Im trockenen Fall (Index wie „dry“) ist die potentielle Temperatur über mit der Entropie verbunden. Die Entropie für trockene Luft ist . Die potentielle Temperatur ist die Temperatur, die ein Luftpaket annehmen würde, wenn man es adiabatisch zu dem Standarddruck von hPa führt: , womit wir auch gleich den Exner-Druck definiert hätten.

Mit dem Begriff der Entropie ist es so eine Sache: Theoretische Physiker interessieren sich für die statistische Darstellung im Boltzmannschen Sinne. Das wollen wir hier nicht tun, sondern ganz bei der klassischen Thermodynamik bleiben. Trotzdem sollte uns die statistische Deutung im Hinterkopf sein, denn sonst bekommen wir keine intuitive Vorstellung von den zu beschreibenden turbulenten Prozessen. In Hajo Langes Lehrbuch „Die Physik des Wetters und des Klimas“ steht ein schöner Satz: „Die Entropie beschreibt die ungeordneten Bewegungen der Moleküle, die sich in dem Sinne herausmitteln, dass kein sich ändernder mechanisch deutbarer Mittelwert übrig bleibt, obwohl diese Bewegungen Energieänderungen des Systems bewirken können.“ Man beachte, was hier nicht gesagt ist: über die Größe des Volumens ist korrekterweise nichts gesagt! In Atkins „Physikalischer Chemie“ steht auch, dass sich in der Umgebung entscheidet, was Arbeit und Wärme ist, also von der Position des Beobachters her, der entscheidet, was Umgebung ist und was nicht.

Zurück zur Anfangsfrage der turbulent zu diffundierenden Variable im Modell. Man sagt:

„Lasst uns die potentielle Temperatur, also die Entropie (im trockenen Fall), über den Mischungswegansatz diffundieren!“

„Wie bitte? Die Entropie diffundieren?“

Ich sage hier nicht, dass das, was seit Jahrzehnten gemacht wird, falsch ist, sondern dass wir die Argumentationskette für das, was wir üblicherweise tun, aufräumen müssen und Feinheiten anpassen müssen. Hier sind offensichtlich einige Begriffe durcheinander gekommen:

• Arbeit
• Wärme
• Entropie
• Auftrieb

Und es muss klar gestellt werden, was ein numerisches Modell nur kann. Ein Modell ist eben nur eine Karikatur der Natur. Aber langsam:

Zunächst müssen wir den Begriff der Volumenarbeit in unserem Kontext klären. Auf Seiten der Impulsgleichung gibt es den Druckgradientterm

   

Die Luft wird beschleunigt oder verlangsamt, also ändert sich deren spezifische kinetische Energie gemäß

   

Nun ist aber der Term genau die Kompressionsarbeit, die die innere Energie eines Luftpakets ändern kann. Beim Zusammendrücken gibt es eine Erwärmung und beim Expandieren eine Abkühlung. Mit diesen Überlegungen sind wir schon bei der Gibbs’schen Fundamentalgleichung. Die innere Energie eines Luftpakets kann sich nur durch Volumenarbeit (weiterhin ist auch die Änderung der chemischen Energie ein Teil der Arbeit) oder prozessierte Wärme ändern. Das heißt, alle Änderungen der inneren Energie, die nicht Arbeit sind, sind prozessierte Wärme und daher mit einer Entropieänderung verbunden. Nur bei reversiblen Prozessen bleibt die Entropie erhalten.

Das Problem bei der numerischen Modellierung ist, dass der Druckgradientterm und der Kompressionsterm über für die menschliche Erfahrungswelt große Skalen berechnet werden müssen, nämlich über die Skala einer Gitterbox. Volumenarbeit kann nur über die aufgelösten Skalen eines Modells dargestellt werden. Alles, was innerhalb eines Gittervolumens an turbulenter kinetischer Energie (TKE) und turbulenter potentieller Energie (TPE, besser: turbulente Auftriebsenergie) vorhanden ist, kann nicht als numerisch aufgelöste Energie mit den entsprechenden Energieumwandlungen dargestellt werden. Daher definiert man die (spezifische) turbulente kinetische Energie: , wobei das Hütchen bedeutet, dass der Mittelwert über die Gitterbox gemeint ist. Das Verrückte ist, dass wir die TKE aus Modellsicht nicht von der (spezifischen) inneren Energie unterscheiden können, in den Messungen aber schon, wir können ja Fluktuationen an einem Punkt messen. Der Pionier der numerischen Wettervorhersage, Lewis Fry Richardson, zählte 1922 daher auch die TKE zur inneren Energie, und nannte dieses Konstrukt intrinsische Energie.

Dies ist ein wichtiger Aspekt, den wir im Zusammenhang mit der kinetischen Gastheorie idealer Gase nochmals vertiefen wollen. Dort betrachtet man den Druck als die Kraft, die die Moleküle auf die Wände eines Volumens ausüben. Das ergibt . Dabei ist schon bedacht, dass das Volumen selbst bewegt sein kann, also eine Lagrangesche Geschwindigkeit hat. Nun betrachte man ein Volumen, worin selbst schon turbulente Bewegungen stattfinden. Man kennt also Temperatur und Geschwindigkeit an feinskaligen Messpunkten und/oder in hoher zeitlicher Auflösung. Dann ist der Druck, den man dem Gesamtvolumen zuschreibt . Diesen Ausdruck kann man unter dem Bedenken, dass für alle Messpunkte je konstant und per Definition ist, umformen zu , also . Die über die Messpunkte gemittelte Temperatur und die TKE sind je über mittlere quadratische Geschwindigkeiten, die jedoch andere Skalen erfassen, definiert. Damit ist die über die Messpunkte gemittelte Temperatur nicht die selbe wie die dem ursprünglichen Volumen zugeschriebene Temperatur . Dieser Unterschied ist in der Praxis winzig und zu vernachlässigen, soll aber vor Augen führen, dass, wenn wir uns mit Thermodynamik beschäftigen, das betrachtete Volumen (der Gitterbox) unser Anhaltspunkt ist, denn für dieses bestimmen wir den Druck. Die Temperatur muss konsistent zu diesem Druck gehören. Damit sind die Begriffe Arbeit und prozessierte Wärme bezüglich der Größen Druck, Temperatur und Volumen genau bestimmt.

Da die TKE eine positiv definite Größe ist, können wir die Analogie zur inneren Energie sogar soweit ziehen, dass wir eine ‚turbulente Wärmekapazität‘ als veränderliche positive Größe definieren und ganz analog zur (spezifischen) inneren Energie schreiben . Diese Auffassung sei hier nur mit dem Verweis angemerkt, dass sie nützlich ist, um später die Gleichungen um einen isothermen Grundzustand linearisieren zu können.

Der turbulente Wärmefluss, der über die Seitenflächen der Gitterboxen fließt, kann nur als die Summe des üblichen Enthalpieflusses und des TKE-Flusses dargestellt werden. Wegen des zweiten Hauptsatzes der Thermodynamik, der besagt, dass Entropie durch interne Prozesse nur zunehmen kann, darf dieser turbulente Wärmefluss, also die Summe der genannten Flüsse, nicht dem Gradienten von (hier ist nicht gemeint) aufwärts fließen. Das ist auf den ersten Blick unintuitiv, da unsere Wahrnehmung von Temperatur erst mal die TKE nicht auf dem Schirm hat. In Atkins „Physikalischer Chemie“ steht aber: „Formal ist die Temperatur eine Größe, die angibt, in welcher Richtung Energie in Form von Wärme fließen wird, wenn wir zwei Systeme über eine wärmeleitende Wand miteinander in Kontakt bringen.“ Die Größenordnungsdefinition der ‚wärmeleitenden Wand‘ ist hier von Belang.

Soweit die Theorie.

Was ist in der Modellierungspraxis zu finden?

• Entwickelt wurde das Turbulenzverständnis mit den Boussinesq-Gleichungen. Die Boussinesq-Gleichungen haben keine mit der Thermodynamik konsistente Energieumwandlungen. Die Energieumwandlungen (i) kinetische Energie in innere Energie und zurück, sowie (ii) kinetische Energie in potentielle Energie und zurück sind „zusammengebacken“. Wir haben es mit der Umwandlung von Auftriebsenergie in kinetische Energie und zurück zu tun. Wenn wir die Auftriebsgröße diffundieren, dann diffundieren wir auch immer das Schwerefeld mit, und das ist unphysikalisch. Explizit wird in der Modellierung mit den vollen Gleichungen (nicht Boussinesq!) korrekterweise über den Mechanismus der massengewichteten Hesselberg/Favre-Mittelung ausgeschlossen, dass Masse diffundiert wird, daher wird dort das Schwerefeld nicht diffundiert.
• Es haben sich zwei Schulen ausgebildet.
  • Die einen benutzen die potentielle Temperatur (oder eine feuchte Variante davon) als die dem Auftrieb verwandteste Größe als prognostische Variable und diffundieren diese potentielle Temperatur: 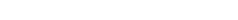. Dieser Vorgang ist aber nicht energieerhaltend. So wird in WRF und MPAS vorgegangen.
  • Die anderen benutzen die Temperatur als prognostische Variable und diffundieren eine Form der statischen Energie: 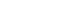im trockenen Fall. Die turbulente Tendenz ist also 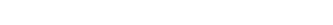. So wird im IFS-Modell vom ECMWF vorgegangen. Im COSMO-Modell steht ähnlicherweise in der Dokumentation: . In dieser Variante ist die Energie erhalten, aber bei stabiler Schichtung kann man feststellen, dass Entropie zerstört und nicht generiert werden könnte. Das sieht man am einfachsten, wenn man die Entropieproduktion als 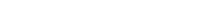ausrechnet und bedenkt, dass bei stabiler Schichtung 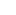mit der Höhe zunimmt, während trotzdem noch die Temperatur mit der Höhe abnehmen kann.
  • Beide Varianten sind also an bestimmten Stellen falsch.
• Oftmals benutzen Modelle eine prognostische TKE-Gleichung, aber lassen den oben diskutierten TKE-Flussterm weg. Die TKE-Gleichung wird nicht zur Gesamtenergetik des Modells gehörend wahrgenommen, sondern nur als Methode, um durch ihren Betrag die Stärke der Turbulenz abzuschätzen.

Der wesentliche Fehler der herkömmlichen Herangehensweise ist, dass die Gesamtenergetik des Modells nicht betrachtet wird und man sich vorrangig auf die Frage, welche passiven Tracer man zu diffundieren hat, fokussiert.

Boussinesq-Approximation

Turbulenz wurde und wird fast immer unter der Boussinesq-Approximation betrachtet. Von der numerischen Seite ist das am feinsten, da man Schallwellen gefiltert hat: die Inkompressibilität ist ein starkes Mittel zum Zweck der effektiven Numerik. Aber was bedeutet die Boussinesq-Approximation eigentlich physikalisch?

Die meiner Meinung nach präziseste Darstellung der Boussinesq Approximation habe ich in Dale Durrans „Numerical Methods for Fluid Dynamics“ gefunden. Dort wird im Gegensatz zu vielen anderen Darstellungen klar, dass es dabei um den Auftrieb und nicht um die Temperatur, und schon gleich gar nicht um Wärme geht. Dale Durran definiert die Druckvariable (pressure) , die Auftriebsvariable (buoyancy) und die Brunt-Väisälä-Frequenz

   

wobei die Querstriche horizontale Mittel bedeuten und schreibt mit diesen Variablen die Boussinesq-Gleichungen ohne diffusive Terme

   

Die zugehörige Boussinesq-Gesamtenergie ist . Hierin gibt es also keine direkt ersichtliche innere Energie, nur kinetische und potentielle Energie, die aber schon genügen, um die gesamten Prozesse, die für den Auftrieb relevant sind, abzubilden. Für den Auftrieb sind Dichteunterschiede relevant. Je weniger dicht ein Luftpaket gegenüber seiner Umgebung ist, desto mehr Auftrieb bekommt es. Es wird sich nach oben beschleunigt bewegen.

Nun schreibt auch Dale Durran, dass diese Form der Boussinesq-Gleichungen mathematisch „schön“ ist, aber ihre qualitative Übereinstimmung mit der Atmosphäre zu wünschen übrig lässt. Die Meteorologen kommen nun mit ihrer potentiellen Temperatur. Aus wird , wobei die virtuelle potentielle Temperatur ist und der Exner-Druck. Der virtuelle Temperaturzuschlag beinhaltet, dass Wasserdampfmoleküle leichter sind als Moleküle der trockenen Luft und Wassertropfen oder Eisteilchen dem positiven Auftrieb entgegen stehen. Die virtuelle potentielle Temperatur ist außer im trockenen Fall nicht zu verwechseln mit der Entropie. Um das klarzustellen, sei folgende Abbildung gezeigt, die vier verschiedene Arten der potentiellen Temperatur an einem Sommertag mit konvektiver Grenzschicht zeigt: die virtuelle potentielle Temperatur (rot), die unter den Meteorologen sehr beliebte äquivalentpotentielle Temperatur (grün) und zwei Varianten einer entropiepotentiellen Temperatur (mit (blau) und ohne (gelb) Hintergrundkonstanten der Entropie für trockene Luft, bzw. Wasserdampf).

Während die virtuelle potentielle Temperatur was mit dem Auftrieb zu tun hat, haben die anderen Varianten damit nichts zu tun. Nur mit der virtuellen potentiellen Temperatur kann man die Boussinesq-Gleichungen in obiger Form benutzen, wenn

   

Nun ist es von den relativen Dichteschwankungen zu den relativen virtuellen potentiellen Temperaturschwankungen nicht weit, und weil die relativen Druckfluktuationen klein sind gegenüber den relativen Temperaturschwankungen, landen wir also bei den relativen Temperaturschwankungen als relevante Größe des Auftriebs. Temperaturschwankungen lassen sich auch leicht messen.

Nun gehen wir mit unserem Ansatz: „Ich muss die turbulenten Diffusionen auf die Tracergröße anwenden“ los:

   

wobei die Fluktuationen anzeigt. Klammheimlich wird dabei aber verbal der auftriebsbedingte Fluss in einen „Wärmefluss“ oder umgewandelt. Man redet immer vom „Wärmefluss“, obwohl es sich hier nicht um fließende Wärme handelt, denn wir hatten ja gesehen, dass wir bei den Boussinesq-Gleichungen die innere Energie (die sich durch , also zum Beispiel die Divergenz der Wärmeflüsse, ändern könnte) nicht von der potentiellen Energie trennen können.

Wie kommen wir jetzt aus dem Dilemma raus, dass die Boussinesq-Gleichungen sehr praktisch und realitätsnah sind, wir von ihnen über die Jahrzehnte viel über Turbulenz gelernt haben, unsere Parametrisierungsansätze von ihnen abstammen, siehe Monin-Obuchow-Theorie, wir aber von ihnen nicht direkt auf die Turbulenzdarstellung im vollen Gleichungssystem schließen dürfen?

A priori Mittelung der Ausgangsgleichungen unter Berücksichtigung einer eigenen Gleichung für die TKE

Jetzt machen wir Nägel mit Köpfen und schauen die vollen Gleichungen für die turbulente feuchte Atmosphäre an.

Wenn man also die Auffassung von Richardsons intrinsischer Energie übernimmt und die TKE mit zur inneren Energie zählt, dann ergibt sich die Gibbs’sche Fundamentalgleichung (in massenspezifischer Schreibweise) zu

   

wobei hier interne und externe Entropieänderungen unterschieden sind. Nur die internen Änderungen beschreiben die Irreversibilität und müssen positiv sein.

Wir bedenken, dass wir ja schon lange die TKE-Gleichung kennen, sie nur nie auf der Ebene der Gesamtenergetik gebraucht haben. Mit ihr ergibt sich das gesamte Gleichungssystem für die Atmosphäre zu

   

Die benutzten Symbole sind ganz unten erklärt. Hier ist erst mal wichtig zu erkennen, dass die TKE-Gleichung explizit auftaucht, während die Gleichung für die turbulente potentielle Energie TPE (Auftriebsenergie) hier nicht explizit zutage tritt. Wir werden gleich sehen, wo sie implizit versteckt ist. Zunächst halten wir fest, dass der klassische sensible Wärmefluss als Summe eines „molekularen“ und eines „turbulenten“ Flusses auftritt , wobei wir den „molekularen“ Anteil nur dort brauchen, wo es keinen „turbulenten“ Fluss gibt. Der „turbulente“ Flussanteil kann nur dort existieren, wo es auch eine TKE gibt. Das bedeutet, dass praktisch nur der Bodenfluss als „molekularer“ Flussanteil gezählt wird, denn am Boden verschwinden alle turbulenten Geschwindigkeiten, aber natürlich nicht die Molekülgeschwindigkeiten.

Die TKE-Gleichung hat einen Auftriebs-Produktions/Verlust-Term

   

An dieser Stelle kommt also die Sortierung nach dem Auftrieb ins Spiel. Die Abweichung von der hydrostatischen Balance regelt die Generierung oder Zerstörung von TKE. Der Auftrieb hat an dieser Stelle nichts mit der Entropiebilanzgleichung zu tun, denn wir sind ja schon dabei, die Prozesse INNERHALB des betrachteten Volumens anzuschauen und NICHT nur den „Fluss über den Rand“-Blick einzunehmen, was die thermodynamischen Hauptsätze allein nur fordern.

Ganz schnell sieht man, dass der Auftriebs-Produktions/Verlust-Term mit einer versteckten TPE-Gleichung Energie über die Divergenz des klassischen sensiblen Wärmeflusses austauscht

   

Der letzte Term ist uns bekannt, er kam schon als subskaliger Term in den Boussinesq-Gleichungen vor:

   

Diese Referenz zu den oben beschriebenen Boussinesq-Gleichungen hilft uns hier sehr, denn die Boussinesq-Gleichungen haben keinen Term für eine Volumenarbeit nach außen, denn bei nur bei ihnen — und nicht bei den vollen Gleichungen — ist . Damit erlaubt ihr subskaliger Term einen Blick in die subskaligen Energieumwandlungen zwischen TKE und TPE. Beide, TKE und TPE, werden zwar ineinander umgewandelt, nach außen erscheint ihr beider gemeinsamer Energiefluss als Wärmefluss.

Der Diffusionsterm der potentiellen Temperaturgleichung multipliziert mit vollzieht also nach, wie TKE und TPE ineinander umgewandelt werden. Energie muss aufgebracht werden, wenn bei stabiler Schichtung turbulente Eddies (Luftballen) vertikal nach oben oder unten verschoben werden sollen. Woher kommt diese Energie? Natürlich aus der TKE. Das heißt, wenn bei stabiler Schichtung der gemessene klassische sensible Wärmefluss nach unten vorhanden ist, wird dafür die TKE genommen, die sich ansonsten durch Diffusion verteilen würde. In der Folge ist die Summe oder sogar dem Temperaturgradienten abwärts und damit mit dem zweiten Hauptsatz konform. Und genau das wird ja auch beobachtet: bei stabiler Schichtung entsteht erst mal durch Scherungsproduktion TKE in Bodennähe und diese kann verwendet werden, um den klassischen sensiblen Wärmefluss am Leben zu erhalten. Ebenso ist in der Schicht an der Obergrenze einer konvektiven Grenzschicht noch TKE vorhanden, die trotz stabiler Schichtung einen klassischen sensiblen Wärmefluss aufrecht erhalten kann.

Wo können die oben genannten Modellfehler von WRF/MPAS bzw. IFS korrigiert werden?

Um diese Frage zu beantworten, schreiben wir die Temperaturgleichung in zwei verschiedenen Varianten auf

   

Die Entweder-Form entspricht dem klassischen turbulenten Mischungsansatz in der -Gleichung, siehe WRF/MPAS. Normalerweise wird aber vergessen, die dissipierte TKE dort hinzuzuaddieren. Es wird auch der Bodenfluss nicht durch den molekularen Fluss dargestellt, sondern der -Term wird einfach auch in der untersten Modellschicht benutzt.

Die Oder-Form fokussiert auf eine Flussbudgetgleichungsform, siehe IFS. Hier sieht man auch den äußeren Scherungsstress an dem Luftvolumen: das ist die Scherungsproduktion der TKE. Wenn man den letzten Term auf die linke Seite schreibt, sieht man, dass er wie eine Temperaturtendenz wirkt . Wenn man für einen Moment konstant lässt und eine lineare Wellenanalyse durchführt, bekommt man linear gedämpfte Wellen für einen Diffusionsansatz für die Temperatur. Im IFS-Modell addiert man den TKE-Fluss nicht und hat auch keinen Term der Tendenz der TKE .

Diskussion

Die beiden genannten Formen sind natürlich physikalisch äquivalent.

Nur in der Oder-Form sieht man den zweiten Hauptsatz schon fast direkt, indem dort der Gesamtfluss als Summe von klassischem sensiblen Wärmefluss plus TKE-Fluss auftaucht und man die Bedingungsfrage: „Ist ?“ direkt auswerten kann.

Mit dem zweiten Hauptsatz steht ein physikalisches Argument zur Verfügung, das es erlaubt, die TKE-Gleichung bei stabiler Schichtung genauer zu spezifizieren und für diesen Fall einen Turbulenzkoeffizienten für die potentielle Temperatur in der Entweder-Form zu bestimmen. Im Fall, dass der Gesamtfluss nicht downgradient T wäre, limitiert man den Gesamtfluss so, dass er verschwindet. Diese Bedingung nutzt man im Auftriebsproduktions/Verlust-Term der TKE-Gleichung. Die Brunt-Väisälä-Frequenz wird dort ersetzt. Man bekommt eine nichtlineare TKE-Gleichung, die negative TKE-Werte verhindert. Wichtig ist der TKE-Flussterm, der downgradient der TKE parametrisiert wird, aber physikalisch vor allem den subskaligen ‚Druckfluss‘-Term und weniger den Fluss der TKE selbst repräsentiert. Die Turbulenz ist nur noch mechanisch getrieben. In der TKE-Gleichung kommt kein thermischer Term mehr vor.

Der positive Auftrieb ist ein Beschleuniger der thermischen Turbulenz und der negative Auftrieb deren Stopper. Der negative Auftrieb limitiert die Turbulenz im Fall des verschwindenden Gesamtwärmeflusses auf ihren mechanischen Anteil. Die Forderung des zweiten Hauptsatzes nach einem Fluss downgradient der Temperatur gibt nur die Richtung des Gesamtflusses, nicht dessen Stärke vor. Die Stärke des Flusses regelt der Auftrieb.

Der Befund, dass bei stabiler Schichtung die thermische Entropieproduktion praktisch Null ergibt, erlaubt es tatsächlich, die Turbulenz in dem Fall als ‚quasi-adiabatisch‘ zu beschreiben. Denn ‚quasi-adiabatisch‘ meint genau das: verschwindende Entropieproduktion, zumindest was deren thermischen Anteil anbetrifft.

Die obige Diskussion macht nochmals klar, dass der Begriff „Wärmefluss“ in der Meteorologie NICHT der klassisch-thermodynamischen Nomenklatur entspricht. Dies hat mich sehr lange gewundert und ich wollte herausfinden, wie die Bezüge zwischen den zwei Begriffen (Teekesselchen) zu beschreiben sind.

Eine ähnliche Begriffsverwirrung gibt es beim Begriff der mechanischen Dissipation. Meteorologen meinen damit die Dissipation der TKE in innere Energie . Von der Perspektive der Modellthermodynamik her ist jedoch die Scherungsproduktion gemeint, denn diese repräsentiert die Scherkräfte, die am betrachteten Volumen (Modellgitterbox) angreifen.

Die diskutierte Darstellung des thermodynamischen Wärmeflusses bleibt auch mathematisch formal wirksam, wenn man die Schwerkraft abschalten würde. Dann gäbe es keinen Auftrieb mehr und die Umwandlung zwischen TKE und TPE spielte keine Rolle mehr. Dann bliebe nur noch der molekulare Wärmefluss downgradient T übrig.

Nachbemerkung

Pascal Marquet hat eine Variante der Brunt-Väisäla-Frequenz für den Fall mit Kondensation entwickelt. Man müsste schauen, ob es dazu eine alternative Variante der zu mischenden Auftriebsvariable gäbe. Das sind aber meiner Meinung nach alles sekundäre — wenn auch für ein echtes Modell wichtige — Überlegungen. Zunächst müssen wir überhaupt ein richtiges Verständnis für die Rolle der irreversiblen Prozesse und ihrer Darstellung im Modell finden.

Glossar

: spec.~turbulent kinetic energy, : constituent (ry, apour, iquid, rozen), : spec.~content of (), : temperature, : spec. internal energy, : spec.~enthalpy, : spec.~entropy, : chemical potential, : shear production with : momentum diffusion tensor and : wind vector, : radiation flux, : sensible heat flux, : tke flux, constituent flux (), constituent source/sink}, , : density, : specific volume, : partial pressure, and : spec. heat capacities at constant pressure and volume, : spec. gas constant, : tke dissipation rate, : buoyancy production and loss, : Exner pressure, : chosen type =(liquid water, virtual, …) potential temperature (), : Bernoulli function, : relative humidities over liquid or frozen water, : enthalpies of vaporization and sublimation.